이 post는 고려대학교 산업경영공학과 DSBA연구실 강필성 교수님의 Business-Analytics강의를 바탕으로 작성되었습니다.
Dimensionality Reduction
오늘은 차원축소에 관한 이야기를 해보겠습니다.
여기서 “차원”이란 독립변수를 의미합니다. 따라서 “차원축소”란 데이터의 독립변수의 개수를 줄이겠다는 뜻입니다. 그렇다면 차원축소를 하려는 이유는 무엇일까요?
당연하게도 그 이유는 model의 성능을 높이기 위함입니다. 이 말을 다시 해석해보면 차원이 너무 많으면 model의 성능이 저하된다는 것을 의미합니다. 이런 현상을 일컬어 우리는 “차원의 저주”라고 부릅니다.
아래는 차원의 개수에 따른 분류기의 성능을 보여주는 그래프입니다. 보시다시피 차원이 일정 수준 이상증가하게 되면 성능이 급격하게 저하되는 것을 알 수 있습니다.

이런 “차원의 저주” 현상이 일어나는 이유는 데이터의 차원이 증가할수록 그 공간의 크기가 기하급수적으로 증가하여 데이터의 밀도 또한 기하급수적으로 희박해지기 때문입니다.
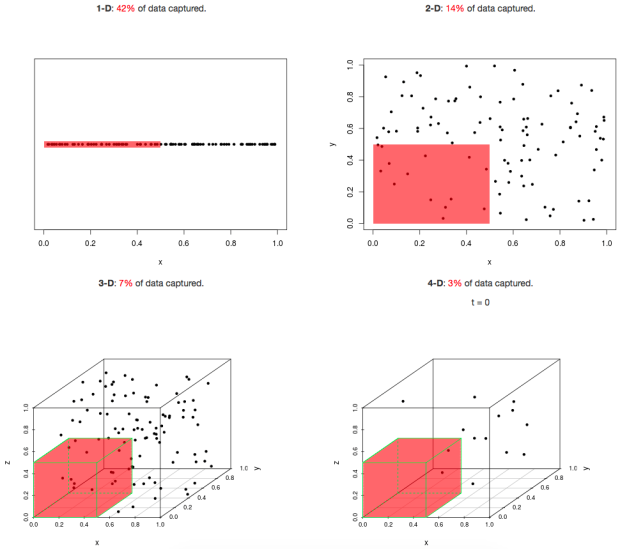
위의 그림처럼 데이터의 밀도가 희박해진다는 것은 결국 데이터 공간에 빈 공간이 많아진다는 뜻입니다. 빈 공간이 많아지게 되면 결국 모델은 점점 해당 공간에서 데이터의 일반적인 특성을 학습하기 어려워지고 그렇기 때문에 모델의 성능이 계속 나빠지는 것입니다.
여기서 오해하면 안되는 것은 모델의 성능은 test 데이터 셋에 대한 성능을 의미한다는 것입니다. 당연하게도 훈련 데이터 셋에 대해서는 차원이 증가할수록 error는 줄어들게 됩니다. (엄밀히 말하면 최소한 error가 커지지는 않습니다.) 결국 “차원의 저주”는 해당 공간을 표현하는 훈련 데이터의 개수에 부족에 따른 과적합의 개념이라고도 볼 수 있습니다.
결론적으로 우리는 “차원축소”를 통해 주어진 독립변수 조합에서 최고의 성능을 보장하는 최적의 조합을 찾고자하는 것입니다.
그렇다면 차원축소의 방법에는 어떤 것들이 있을까요?
아래의 그림은 이를 잘 정리하여 보여줍니다.
Feature Selection은 기존의 독립변수를 취사선택하여 사용하는 방법론이고, Feature Extraction은 데이터로부터 새로운 독립변수를 생성하여 사용하는 방법론입니다.
Feature Selection의 경우 기존의 독립변수들로 만들어질 수 있는 조합 중 최적의 조합을 선택하는 것이 목적입니다. 따라서 그 조합의 성능을 평가하는 지표가 필요합니다.
Filter의 경우 Class Label만을 활용하여 Information Gain, Odds ratio등의 지표를 계산해 조합을 선택합니다. Wrapper의 경우에는 지표를 따로 계산하는 것이 아니라 Learning Algorithm을 통해 그 조합의 성능을 평가합니다. 그렇기때문에 어떤 Learning Algorithm을 쓰느냐에 따라서 결과가 달라질 수 있습니다.
Feature Extraction의 경우 기존의 데이터를 통해 새로운 차원을 생성하게 됩니다. 따라서 어떤 차원을 생성할 것인지 기준을 정해야 합니다.
가장 널리 알려진 PCA의 경우 그 기준은 분산입니다. 즉 PCA는 기존의 데이터의 분산을 최대한 보존하는 새로운 축을 찾고자 하는 방법론입니다. 그 밖에도 그 기준을 어떻게 삼느냐에 따라서 MDS, ISOMAP, LLE등 다양한 방법론들이 존재합니다.
이렇게해서 우리는 “차원 축소”에 대한 기본적인 지식을 학습하였습니다.
이제부터는 차원축소(Dimensionality Reduction)의 방법 중 한 갈래인 Supervised Method방법에 대해서 알아보도록 하겠습니다.
Forward Selection
오늘 소개해드릴 차원축소의 Supervised Method는 바로 Forward Selection, Backward Elimination, Stepwise Selection, 그리고 Genetic Algorithm입니다.
위의 방법론들을 소개하기에 앞서 Exhaustive Search라는 방법론을 소개해드리겠습니다. 거창하게 말했지만 사실 이 방법론은 단순히 가능한 모든 독립변수의 조합을 전부 탐색해보는 방법을 말합니다.
위의 그래프를 보시면 초당 10,000개의 조합을 탐색할 수 있다고 가정해도 변수의 개수가 40개를 초과하는 순간부터 현재 시점과 빅뱅이 일어난 시점의 차이 만큼의 시간이 필요하게 됩니다. 따라서 변수의 개수가 조금만 많아도 Exhaustive Search는 현실적으로 불가능합니다.
지금부터 소개할 4가지의 method는 휴리스틱 기반의 방법론으로 optimal을 보장하지는 못하지만 Exhaustive Search와는 달리 변수의 개수가 많아도 현실적으로 실행 가능합니다. 또한 이 method들은 마구잡이식으로 탐색하는 것이 아니라 전략적으로 탐색하기 때문에 optimal은 아닐지라도 optimal에 가까운 대안을 도출할 확률이 높은 방법론이라고 할 수 있습니다.
이제부터는 본격적으로 각 Method에 대하여 알아보도록 하겠습니다.
Forward Selection
Forward Selection
다음 그림은 Forward Selection의 절차입니다.
Forward Selection은 변수가 하나도 없는 상태로부터 시작해서 1개씩 변수를 추가합니다. 추가할 변수는 fitness function에 의해 결정됩니다. 즉 추가했을 때 fitness function이 가장 높은 값을 가지는 변수를 선택하는 방식입니다. 이 방법론에서는 한 번 추가된 변수는 절대 제거되지 않습니다. 따라서 단계가 진행될수록 변수가 1개씩 추가됩니다.
이 알고리즘을 끝까지 수행하면 결국 우리는 모든 변수를 선택해 집어넣게 될 것입니다. 그렇기때문에 차원축소의 효과를 보기 위해서는 언제 알고리즘을 종료할지에 대한 기준인 Stopping Criteria를 설정해야 합니다.
이런 기준을 설정하는 것은 사용자의 자유이며 상황에 따라 달라질 수 있습니다. 따라서 보편적으로 사용되는 기준들에 대해서 간략하게 설명하고 넘어가도록 하겠습니다.
1) 성능이 기준 이상을 만족
2) 성능이 증가하다가 변수를 추가하여도 더 이상 성능이 증가하지 않음
3) 성능이 좋아질 여지가 있지만 변수의 개수가 일정 개수를 초과
일반적으로 기준 2)가 가장 많이 쓰이지만 답이 정해져있지 않은 부분으로 실무자의 판단에 따라서 얼마든지 바뀔 수 있습니다.
이론적으로 이 알고리즘의 최대 계산량은 N(N+1)/2입니다.
Forward Selection
Backward Elimination
다음 그림은 Backward Elimination의 절차입니다.
이 알고리즘은 Forward Selection과는 반대로 모든 독립변수를 포함한 상태에서 시작해서 1개씩 변수를 제거합니다. 마찬가지로 제거할 변수는 fitness function에 의해 결정됩니다. 즉 제거했을 때 fitness function이 가장 높은 값을 가지는 변수를 조합에서 제외합니다. Forward Selection과 마찬가지로 한번 제거된 변수는 다시 선택되지 않습니다.
다음은 Backward Elimination에서 보편적인 Stopping Criteria입니다.
1) 성능이 기준 이하로 내려감
2) 성능이 증가하다가 변수를 제거하여도 더 이상 성능이 증가하지 않음
이 알고리즘도 이론적으로 최대 계산량은 N(N+1)/2입니다.
Forward Selection
Stepwise Selection
다음 그림은 Stepwise Selection에 대한 절차입니다.
이 알고리즘은 Forward Selection과 Backward Elimination의 방식을 번갈아가며 사용합니다.
초기상태는 Forward Selection과 동일합니다. 따라서 변수가 3개가 되기전까지는 Forward Selection만 진행되고 그 이후에 Forward Selection과 Backward Elimination을 번갈아 수행하게 됩니다. 두 방식을 모두 사용하기 때문에 Stepwise Selection에서는 한번 추가(혹은 제거)되었던 변수일지라도 다시 제거(혹은 추가)될 수 있습니다.
이 방식은 당연하게도 앞선 두 방식보다 더 많은 계산량을 필요로 합니다. 하지만 앞선 방식보다 탐색 범위가 넓기 때문에 성능이 좋은 조합을 찾을 확률이 높습니다.
Forward Selection
Genetic Algorithm
이 알고리즘은 “메타 휴리스틱”이라고 불리는 기법으로 염색체의 유전 과정을 모방하여 만들어진 기법입니다. GA는 오늘 소개하는 Method중 가장 계산량이 높지만 그만큼 효율적으로 더 많은 범위의 조합을 탐색할 수 있는 알고리즘입니다.
이 알고리즘의 단계는 다음과 같습니다.
1) 파라미터 설정 및 염색체 초기화
2) 각 염색체 선택 변수별 모델학습
3) 각 염색체 적합도 평가
4) 우수 염색체 선택
5) 다음 세대 염색체 생성
6) Stopping criteria 만족 O: 최종 변수 집합 선택 or Stopping criteria 만족 X: Step 2부터 다시 진행
이제 각 단계별로 자세히 알아보도록 하겠습니다.
Forward Selection
1) 파라미터 설정 및 염색체 초기화
GA를 실행하기 위해서는 가장 먼저 아래의 Parameter값에 대하여 설정해주어야 합니다.
-
Population: 한 세대에 몇 개의 염색체를 포함시킬지 정해주어야 합니다.
-
Fitness function: 모델의 성능을 평가하는데 어떤 지표를 쓸지 정해주어야 합니다.
-
Crossover mechanism: 어떤 규칙으로 Crossover를 진행할지 정해주어야 합니다.
-
The rate of mutation: 돌연변이를 얼마만큼 허용할지 정해주어야 합니다.
-
Stopping criteria
crossover와 muation의 개념은 뒤에서 자세히 설명하오니 당황하지 않으시길 바랍니다.
파라미터에 대한 설정이 끝나면 Population의 수만큼 염색체를 초기화해야 합니다. “차원축소”를 위해 GA를사용하는 경우 염색체는 독립변수의 조합을 의미하게 됩니다.
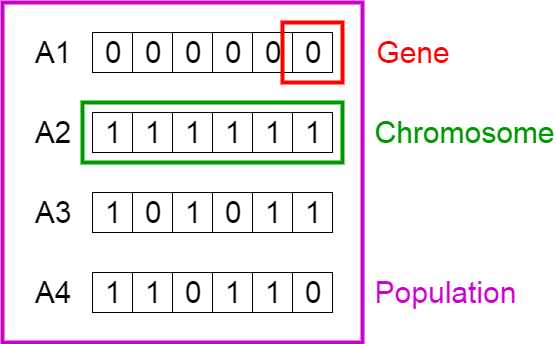
위의 그림을 보시면 빨간색으로 표시된 것은 유전자(=독립변수)이고, 그것들이 모여 초록색으로 표시된 염색체(=독립변수의 조합)을 구성하게 됩니다. 염색체의 유전자의 값은 해당 독립변수에 대한 사용여부를 나타냅니다. 보통 1인 경우 사용함을 의미하고 0인 경우는 사용하지 않는 것을 의미합니다.
일반적으로 50:50의 비율로 random하게 0과 1을 할당하여 초기화를 한다고 합니다.
Forward Selection
2) 각 염색체 선택 변수별 모델학습
이 단계에서는 각 염색체 선택 변수별 모델을 학습하게 됩니다.
Forward Selection
3) 각 염색체 적합도 평가
우리가 설정한 fitness function으로 각 염색체의 성능을 평가하는 단계입니다. 이 때 일반적으로 같은 성능을 가진 염색체의 경우 선택된 변수의 개수가 더 적은 염색체가 더 좋은 염색체라고 판단합니다.
Forward Selection
4) 우수 염색체 선택
이제 다음 세대의 population을 구성하기 위해 우수 염색체를 선택하여야 합니다. 우수 염색체를 선택하는 방법에는 크게 2가지가 있습니다.
- Deterministic selection
- 적합도 기준으로 상위 N%의 염색체 중에서 random하게 2개 선택
- 하위 (100-N)%의 염색체는 절대로 선택되지 않음
- Probailistic selection
- 적합도에 비례하여 염색체별로 가중치를 할당
- 가중치에 비례한 확률로 2개의 염색체를 선택
Deterministic한 방법과 Probabilistic한 방법 중 이론적으로 어떤 것이 뛰어난지는 밝혀지지 않았습니다. 제 개인적인 의견으로는 Probabilistic한 방법이 좀 더 탐색영역이 넓어 성능이 좋을 것이라고 기대됩니다.
이런 제 개인적인 의견을 뒷받침하는 논문이 하나 있는데 1995년에 발표된 “Comparison of probabilistic and deterministic optimizations using genetic algorithms“라는 논문입니다.
논문에서는 “The main reason is that probabilistic optimization is more effective than deterministic optimization in accounting for differences in the scatter of random variables and the resulting differences in the importance of failure modes.”라고 말을 합니다. 즉 Deterministic 방법보다 좀 더 넗은 범위에서 우수 염색체를 선택하기 때문에 성능이 우수하였다는 뜻입니다.
하지만 역시 이론적으로 증명된 부분이 아니기 때문에 어떤 데이터와 모델을 사용하느냐에 따라서 결과가 달라질 수 있음을 인지하고 계셔야 할 것입니다.
Forward Selection
5) 다음 세대 염색체 생성
이제 우수 염색체 2개를 선택했으니 이 2개의 부모 염색체를 통해 2개의 자식 염색체를 생성해야 합니다. 자식 염색체는 crossover와 mutation의 과정을 거쳐 생성되게 됩니다. 차례대로 설명해보도록 하겠습니다.
-
Crossover

crossover를 하기위해서는 crossover point를 지정해야 합니다. crossover point를 기준으로 부모 염색체 간 서로의 염색체를 교환할지 정하게 되기 때문입니다. 이 때 교환은 확률적으로 일어나며 보통 50% 확률로 교환이 일어나도록 설정한다고 합니다.
-
Mutatuion

mutation은 각 염색체 cell별로 일어납니다. 일정 확률로 각 염색체 cell이 1->0 혹은 0->1로 바뀌게 됩니다. 그 확률을 너무 높게 설정하면 부모 염색체로부터 형질을 물려받는 의미가 없어지기 때문에 보편적으로 0.01의 확률로 mutation이 일어나도록 설정하는 것이 좋다고 합니다.
이렇게 crossover와 mutation이 끝나면 총 2개의 자식 염색체가 생성됩니다. 생성된 자식 염색체는 다음 세대의 구성원이 됩니다.
단계 4)와 5)는 다음 세대의 population이 기존에 설정했던 population의 수를 모두 채워질때 까지 반복됩니다. 이 때 일반적으로 이전 세대에서 가장 성능이 좋았던 염색체는 보존하여 다음 세대로 포함시킨다고 합니다.
Forward Selection
6) Stopping criteria 만족 O: 최종 변수 집합 선택 or Stopping criteria 만족 X: Step 2부터 다시 진행
다음 세대의 population이 구성되면 stopping criteria를 통해 최종 변수 집합을 선택할지 아니면 step2부터 다시 진행할지 결정하여야 합니다. stopping criteria는 보통 목표 성능을 만족하거나 일정 이상의 반복회수가 초과되는 것을 기준으로 합니다.
이렇게해서 GA 알고리즘의 절차에 대해서 모두 학습하였습니다. 마지막으로 한가지 더 말씀드리면 GA 알고리즘의 경우 큰 성능 향상은 초기단계에 이루어지고 뒤로갈수록 그 폭이 줄어들어 아래와 같은 그래프를 그리게 된다고 합니다.

Forward Selection
Performance Metrics
지금까지 차원축소에 관한 4가지 기법을 학습하였습니다. 4가지 기법 모두 변수를 선택하기 위하여 각 조합에 대한 모델의 performance(혹은 fitness)를 구하는 과정이 있습니다. 이제부터는 모델의 performace를 구하기 위한 지표에는 어떤 것들이 있는지 살펴보도록 하겠습니다.
-
Adjusted R-squared
단순 R-squared의 경우 독립변수의 개수가 증가하면 SSE가 감소하여 함수 값도 증가하기 때문에 차원축소의 지표로 사용하기에는 부적절합니다. 그렇기 때문에 독립변수의 개수를 고려할 수 있도록 변형한 Adjusted R-squared을 사용하는 것이 좋습니다.
식을 보시면 알 수 있듯이 Adjusted R-squared의 경우 독립변수의 k가 증가하여 SSE가 줄어도 분모에 있는 n-k-1식이 감소하기 때문에 SSE가 줄어든 것을 보완합니다.
-
Akaike Inforamtion Criteria (AIC)
AIC는 SSE를 기반이지만 독립변수의 개수에 비례하여 penalty를 가집니다. 그 식은 다음과 같습니다.
AIC의 경우 값이 낮을수록 적합도가 높은 모형입니다.
-
Bayesian Information Criteria(BIC)
BIC는 AIC가 다른 표본을 사용할 경우 공식모형이 달라서 비교가 불가능하다는 단점을 보완하기 위해 표본 크기를 반영한 지표입니다. 따라서 BIC를 사용하면 서로 다른 표본으로도 경쟁모형의 비교가 가능합니다.
AIC와 마찬가지로 값이 낮을수록 적합도가 높은 모형입니다.
Forward Selection
Empirical Study
이렇게해서 차원축소의 4가지의 기법과 그 기법들을 실행하는데 쓰이는 performance metirc들에 대해서 모두 알아보았습니다.
이제 마지막으로 각 기법들이 실제로 performance의 측면에서 얼마나 우수한지 검증했었던 실험 결과들에 대해서 알아보도록 하겠습니다.
위는 실험에 사용되었던 49개의 Dataset을 나열한 것입니다.
왼쪽은 Error를 얼마나 감소시켰는지에 대한 그림이고 오른쪽은 차원축소가 얼마만큼 일어났는지 그 비율에 대한 그림입니다. 왼쪽의 경우 빨간색에서 파란색으로 갈수록 에러율이 줄어든 것이고 오른쪽의 경우에는 색이 짙을수록 변수가 제거된 비율이 높은 것입니다.
각 기법들에 대해 평균적으로 에러 감소율, 차원축소율, 계산 효율성에 관해 순위를 매기면 위와 같습니다. 여기서 Ridge, LASSO, Enet는 여기서는 다루지 않았으니 참고만 하시면 되겠습니다.
성능은 GA-Stepwise-Backward-Forward순이였고, 차원축소율은 Stepwise-Backwrad-Forward-GA순이였습니다. 그리고 계산 효율성은 Forward-Backward-Stepwise-GA순이였습니다. 최대 계산량이 동일함에도 불구하고 Backward의 계산 효율성이 Forward보다 나쁜 이유는Backward의 경우 처음부터 모든 변수를 추가한 상태에서 모델을 구성해야 하기 때문입니다.
성능과 계산효율성 순위가 정확히 반대인데, 이는 더 넓은 범위를 탐색하는 알고리즘이 계산 효율성은 떨어지지만 좀 더 높은 성능을 보장한다는 것을 보여줍니다.
Forward Selection
Example in python
이제 마지막으로 각 기법들을 R을 통해 실습해보도록 하겠습니다.
각 기법들을 적용할 learning algorithm으로는 회귀분석을 사용하였습니다. 데이터는 Kaggle 사이트의 “House Sales in King County, USA” 데이터를 사용하였습니다. 데이터는 21613개의 object로 구성되어 있습니다.
모델을 구성하는데 사용할 데이터의 각 변수에 대해서 설명하도록 하겠습니다.
- Price: Pirce is prediction targe
- Bedrooms: Number of bedrooms (factor)
- Bathrooms: Number of bathrooms (factor)
- sqft_living: Square footage of the home
- sqft_lot: Square footage of the lot
- sqft_basement: Square footage of the basement
- Floors: Total floors in house (factor)
- Waterfront: House which has a view to a waterfront
- view: Number of Has been viewed
- condition How good the condition is (factor)
- grade: Overall grade given to the housing unit, based on King County grading system (factor)
- sqft_above: Square footage of house apart from basement
- lat: 위도
- long: 경도
이렇게 1개의 종속변수와 13개의 독립변수를 사용하였습니다.
이제부터 본격적으로 각 기법을 구현한 python code를 살펴보도록 하겠습니다.
-
구현에 필요한 패키지 import하기 및 데이터 불러오기
import numpy as np import pandas as pd import random import statsmodels.formula.api as sfstatsmodels.formula.api는 회귀분석 모델을 구현하는데 사용된 모듈입니다.
data = pd.read_csv("kc_house_data.csv", sep=",")pd.read_csv함수를 사용하여 제 작업공간안에 있는 data를 불러왔습니다.
-
Variable Selection [forward, backward, stepwise]
파이썬에서는 따로 각 기법을 구현한 패키지가 존재하지 않기 때문에 직접 구현하여야 합니다. 저는 forward, backward, stepwise 알고리즘의 구조가 서로 비슷하므로 하나의 함수를 지정해 3가지 기법을 모두 구현하였습니다.
def variable_selection(data,target,direction): var = set(data.columns) var.remove(target) current_score, best_new_score = 0.0, 0.0variable_selection이라는 함수명을 사용하였습니다. 전달받을 인자로는 회귀분석에 사용할 data, 그 data의 종속변수인 target, 그리고 어떤 기법을 사용할지에 대한 direction값을 받았습니다.
각 기법들에 대한 코드를 작성하기 전에 먼저 데이터의 독립변수들의 이름을 var라는 함수에 저장하였습니다. 또한 현재의 fittness value를 저장하는 current_score와 새로운 변수가 추가(혹은 제거) 되었을 때 fittness value가 가장 높은 것을 저장하는 best_new_score라는 변수를 생성하였습니다.
if direction == "forward": inmodel =[] outmodel = var while outmodel and current_score==best_new_score: score_candidate = [] for candidate in outmodel: formula = "{}~{}+1".format(target,'+'.join(inmodel+[candidate])) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.remove(best_candidate) inmodel.append(best_candidate) current_score = best_new_score formula = "{}~{}+1".format(target,'+'.join(inmodel)) model = sf.ols(formula, data).fit() return modelforward 알고리즘은 함수가 direction값을 “forward”로 전달받았을 때 실행되도록 하였습니다.
현재 model에 포함되어 있는 독립변수를 나타내는 inmodel변수와 그렇지않은 변수들을 나타내는 outmodel 변수를 생성하였습니다. forward 알고리즘의 경우 초기상태일 때 모델안에 변수가 없으므로 inmodel 값으로 빈 list를 지정하였고, outmodel 값으로 var을 전달받았습니다.
while함수를 사용하여 outmodel에 아직 독립변수가 남아있고, current_score가 best_new_score의 값과 같은 경우 loop를 실행하도록 설정하였습니다. 여기서 current_score가 best_new_score와 같다는 것은 알고리즘이 1번 실행된 결과 model의 적합도가 향상되었음을 의미합니다. 즉 만약 두개의 값이 같지 않다면 적합도가 실행되지 않은 것이므로 loop를 중단합니다.
while loop의 첫 부분에는 score_candidate라는 빈 리스트를 생성하여 각 독립변수를 모델에 추가하였을 때 적합도 값과 그 독립변수를 저장하도록 하였습니다.
for문을 통하여 outmodel에 있는 독립변수들을 하나씩 추가해가며 model을 구성하고 그 값과 그 때의 독립변수를 score_candidate에 append하였습니다.
그 후 score_candidate을 sort() 함수를 이용해 정렬하였고, pop() 함수를 이용하여 가장 높은 적합도 값과 그 때의 독립변수를 각각 best_new_score와 best_candidate이라는 변수에 저장하였습니다.
if문을 통해 best_new_score값이 current_score값보다 크면 즉 적합도 값이 향상되었으면 그 독립변수를 outmodel에서 제거하고 inmodel에 추가하였습니다. 그리고 current_score 변수에 best_new_score값을 대입하였습니다.
이렇게해서 while문을 다돌고 바져나오게 되면 sf.ols라는 함수를 통해 회귀모델을 만들고 그 모델을 반환하도록 하였습니다.
elif direction == "backward": inmodel = var outmodel = [] while inmodel and current_score==best_new_score: score_candidate = [] for candidate in inmodel: formula = "{}~{}+1".format(target,'+'.join(inmodel-set(candidate))) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.append(best_candidate) inmodel.remove(best_candidate) current_score = best_new_score formula = "{}~{}+1".format(target,'+'.join(inmodel)) model = sf.ols(formula, data).fit() return modelbackward 알고리즘은 direction값을 “backward”로 전달받았을 때 실행됩니다.
위 코드는 inmodel 과outmodel값이 서로 반대가 되고 각 단계마다 inmodel에 변수가 추가되는 것이 아니라 제거된다는 점을 빼면 forward 알고리즘의 코드와 똑같습니다. 차근차근 살펴보시면 쉽게 이해하실 수 있을겁니다.
elif direction == "stepwise": inmodel =[] outmodel = var outmodel = list(outmodel) count = 0 stop = 0 while outmodel and stop<2: score_candidate = [] count=count+1 if count%2 ==1 or count==2: for candidate in outmodel: formula = "{}~{}+1".format(target,'+'.join(inmodel+[candidate])) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.remove(best_candidate) inmodel.append(best_candidate) current_score = best_new_score stop=0 else: stop=stop+1 else: for candidate in inmodel: formula = "{}~{}+1".format(target,'+'.join(set(inmodel)-set(candidate))) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.append(best_candidate) inmodel.remove(best_candidate) current_score = best_new_score stop=0 else: stop=stop+1 formula = "{}~{}+1".format(target,'+'.join(inmodel)) model = sf.ols(formula, data).fit() print(count) return modelstepwise 알고리즘은 direction값을 “stepwise”로 전달받았을 경우 실행됩니다.
초기상태는 forward 알고리즘과 똑같기 때문에 inmodel에는 빈 리스트가 outmodel에는 var가 저장되었습니다. var가 집합자료형인 것이 문제가되어 이 경우에는 list자료형으로 변환 후 사용하였습니다.
stepwise 알고리즘은 forward와 backward 알고리즘을 번갈아가며 수행하는 알고리즘이기 때문에 코드의 대부분의 내용이 위에서 설명한 것들입니다. 따라서 이 알고리즘에서만 새롭게 추가되거나 변경된 점에 대해서만 짚어보도록 하겠습니다.
우선 count변수 입니다. count변수는 각 loop마다 1이 더해집니다. 따라서 stepwise 알고리즘이 몇 번 실행됬는지 알려줍니다. 또한 forward와 backward를 번갈아가며 수행하기 위하여 count값을 2로 나눈 경우 나머지가 1이면 forward 0이면 backward를 실행하도록 하였습니다. (count=2인 경우 forward를 수행하도록 한 것은 backward를 해봤자 적합도가 향상되지 않을 것이 자명하기 때문입니다.)
stop변수도 새롭게 추가되었습니다. stop변수는 forward 혹은 backward 알고리즘을 수행 후 적합도의 향상이 일어나지 않은 경우 1이 더해지고, 그렇지않다면 0을 대입합니다. 따라서 while 함수에 stop<2라는 조건을 추가하여 어떤 시점에서 forward 혹은 backward를 모두 실행했는데 적합도가 향상되지 않은 경우 loop를 끝내도록 하였습니다.
그리하여 전체 코드는 다음과 같습니다.
def variable_selection(data,target,direction): var = set(data.columns) var.remove(target) current_score, best_new_score = 0.0, 0.0 if direction == "forward": inmodel =[] outmodel = var while outmodel and current_score==best_new_score: score_candidate = [] for candidate in outmodel: formula = "{}~{}+1".format(target,'+'.join(inmodel+[candidate])) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.remove(best_candidate) inmodel.append(best_candidate) current_score = best_new_score formula = "{}~{}+1".format(target,'+'.join(inmodel)) model = sf.ols(formula, data).fit() return model elif direction == "backward": inmodel = var outmodel = [] while inmodel and current_score==best_new_score: score_candidate = [] for candidate in inmodel: formula = "{}~{}+1".format(target,'+'.join(inmodel-set(candidate))) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.append(best_candidate) inmodel.remove(best_candidate) current_score = best_new_score formula = "{}~{}+1".format(target,'+'.join(inmodel)) model = sf.ols(formula, data).fit() return model elif direction == "stepwise": inmodel =[] outmodel = var outmodel = list(outmodel) count = 0 stop = 0 while outmodel and stop<2: score_candidate = [] count=count+1 if count%2 ==1 or count==2: for candidate in outmodel: formula = "{}~{}+1".format(target,'+'.join(inmodel+[candidate])) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.remove(best_candidate) inmodel.append(best_candidate) current_score = best_new_score stop=0 else: stop=stop+1 else: for candidate in inmodel: formula = "{}~{}+1".format(target,'+'.join(set(inmodel)-set(candidate))) score = sf.ols(formula,data).fit().rsquared_adj score_candidate.append((score,candidate)) score_candidate.sort() best_new_score, best_candidate = score_candidate.pop() if current_score<best_new_score: outmodel.append(best_candidate) inmodel.remove(best_candidate) current_score = best_new_score stop=0 else: stop=stop+1 formula = "{}~{}+1".format(target,'+'.join(inmodel)) model = sf.ols(formula, data).fit() print(count) return model else: print("forward,backward,stepwise중에서 입력하시오")맨 밑 코드를 보시면 direction을 잘못 입력한 경우 “forward,backward,stepwise중에서 입력하시오” 과 같은 문구를 출력하도록 하였습니다.
-
GA
GA 알고리즘을 구현한 GA 함수를 소개하기전에 crossover와 mutation의 과정을 거쳐 2개의 자식 염색체를 생성하는 cro_mut라는 함수에 대해서 설명하도록 하겠습니다.
def cro_mut(mother, father,crossover,mutation,length): index=[0] index=index+random.sample(range(1,length),crossover) index=index+[length] child1=mother child2=father for i in range(crossover+1): if random.sample(range(2),1)[0]: index2=index[i] index3=index[i+1] child1[index2:index3]=father[index2:index3] child2[index2:index3]=mother[index2:index3] for i in range(length): temp=random.sample(range(mutation),1)[0] if temp==0: if child1[i]==0: child1[i]=1 else: child1[i]=0 for i in range(length): temp=random.sample(range(mutation),1)[0] if temp==0: if child2[i]==0: child1[i]=1 else: child2[i]=0 return [child1,child2]위 cro_mut라는 함수는 부모 염색체인 mother과 father, crossover point의 개수를 나타내는 crossover, mutation이 확률적으로 몇 번중에 1번 발생하는지를 나타내는 mutation값 그리고 사용할 데이터의 독립변수의 총 개수를 나타내는 length값을 인자로 받습니다.
위 함수는 crossover가 진행될 지점의 값을 index라는 list에 저장하고 if random.sample(range(2),1)[0]라는 조건문을 통해 50%의 확률로 crossover가 일어나도록 하였습니다. mutation은 각 염색체 cell마다 반복문을 돌아서 미리 지정한 확률에 따라 발생하도록 하였습니다.
함수는 최종적으로 2개의 자식 염색체를 반환합니다.
def GA (data, target, iteration, population, crossover, mutation): for i in range(iteration): ###첫 세대 구성 if i==0: var = set(data.columns) var.remove(target) var=list(var) var_length = len(set(data.columns))-1 one = np.ones((population,round(var_length/2))) zero = np.zeros((population,var_length-round(var_length/2))) old = [] temp = np.hstack([one,zero]) temp = temp[0] for ind in range(population): random.shuffle(temp) old.append(list(temp)) ###염색체별 모델 구성 및 평가 score = [] for ind in range(population): temp=old[ind] inmodel=[] for ind2 in range(len(temp)): if temp[ind2]: inmodel.append(var[ind2]) formula = "{}~{}+1".format(target,'+'.join(inmodel)) score.append((sf.ols(formula,data).fit().rsquared_adj,temp)) score.sort() next_population=[] ###best 염색체 2개 보존 next_population.append(score[-1][1]) next_population.append(score[-2][1]) ###Deterministic approch parent_set = score[round(0.7*population):] ###다음 세대 구성 while len(next_population)<population: m=random.randrange(0,len(parent_set)) f=random.randrange(0,len(parent_set)) mother=parent_set[m][1] father=parent_set[f][1] next_population= next_population+cro_mut(mother,father,crossover,mutation,var_length) old = next_population ###반복이 종료된 후 마지막 세대의 best 염색체 선정 및 모델 반환 for ind in range(population): temp=old[ind] inmodel=[] for ind2 in range(len(temp)): if temp[ind2]: inmodel.append(var[ind2]) formula = "{}~{}+1".format(target,'+'.join(inmodel)) score.append((sf.ols(formula,data).fit().rsquared_adj,temp)) score.sort() temp=score[-1][1] for ind2 in range(len(temp)): if temp[ind2]: inmodel.append(var[ind2]) formula = "{}~{}+1".format(target,'+'.join(inmodel)) model=sf.ols(formula,data).fit() return modelGA 함수는 회귀분석에 사용할 data, data의 종속변수인 target, 알고리즘의 총 반복횟루를 의미하는 iteration, population의 크기 그리고 cro_mut 함수에 사용될 crossover와 mutation을 인자로 받습니다.
GA 함수는 실행되면 for i in range(iteration)를 통해 사용자가 지정한 반복 횟수만큼 실행됩니다.
가장 첫 번째 반복시에는 old라는 리스트에 0과 1로 구성된 염색체들을 random.shuffle()함수를 사용하여 population의 크기만큼 할당합니다.
그 이후부터는 세대안의 염색체 별로 모델을 구성하고 평가하는 part, 다음 세대의 자식 염색체를 생성하는 part 그리고 반복이 종료된 후 최종적으로 가장 좋은 모델을 반환하는 part로 이루어져있습니다. 각 part는 단순히 반복문을 통해 구현하였기 때문에 수월하게 이해하실 수 있을겁니다.
저는 crossover를 하는데 있어 Diterministic한 방법을 사용하였고 이전 세대에서 가장 적합도가 우수한 2개의 염색체는 다음 세대로 보존하였습니다.
-
결과
앞서 언급한 data를 가지고 함수들을 실행시켜보도록 하겠습니다.
model=variable_selection(data,"price","forward") print(model.summary())OLS Regression Results ============================================================================== Dep. Variable: price R-squared: 0.674 Model: OLS Adj. R-squared: 0.674 Method: Least Squares F-statistic: 4054. Date: Thu, 25 Oct 2018 Prob (F-statistic): 0.00 Time: 22:24:37 Log-Likelihood: -2.9550e+05 No. Observations: 21613 AIC: 5.910e+05 Df Residuals: 21601 BIC: 5.911e+05 Df Model: 11 Covariance Type: nonrobust =============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------- Intercept -6.167e+07 1.4e+06 -44.089 0.000 -6.44e+07 -5.89e+07 sqft_living 173.5111 4.436 39.114 0.000 164.816 182.206 lat 6.475e+05 1.06e+04 60.971 0.000 6.27e+05 6.68e+05 view 6.093e+04 2179.234 27.957 0.000 5.67e+04 6.52e+04 grade 8.397e+04 2082.713 40.316 0.000 7.99e+04 8.8e+04 waterfront 5.909e+05 1.81e+04 32.729 0.000 5.55e+05 6.26e+05 condition 5.233e+04 2305.797 22.696 0.000 4.78e+04 5.69e+04 long -2.477e+05 1.12e+04 -22.155 0.000 -2.7e+05 -2.26e+05 bedrooms -3.023e+04 1957.597 -15.441 0.000 -3.41e+04 -2.64e+04 sqft_above 38.7132 4.486 8.629 0.000 29.920 47.506 floors -2.845e+04 3608.128 -7.884 0.000 -3.55e+04 -2.14e+04 bathrooms 6398.9994 3191.489 2.005 0.045 143.444 1.27e+04forward 알고리즘을 실행한 결과 총 13개의 독립변수 중에서 11개의 독립변수가 선택되었습니다. R-squared의 값은 0.674입니다.
model=variable_selection(data,"price","backward") print(model.summary())Dep. Variable: price R-squared: 0.658 Model: OLS Adj. R-squared: 0.657 Method: Least Squares F-statistic: 3770. Date: Thu, 25 Oct 2018 Prob (F-statistic): 0.00 Time: 22:26:20 Log-Likelihood: -2.9602e+05 No. Observations: 21613 AIC: 5.921e+05 Df Residuals: 21601 BIC: 5.922e+05 Df Model: 11 Covariance Type: nonrobust ================================================================================= coef std err t P>|t| [0.025 0.975] --------------------------------------------------------------------------------- Intercept -6.223e+07 1.46e+06 -42.623 0.000 -6.51e+07 -5.94e+07 lat 6.421e+05 1.09e+04 58.915 0.000 6.21e+05 6.63e+05 sqft_lot -0.0122 0.037 -0.330 0.741 -0.085 0.060 long -2.545e+05 1.16e+04 -21.884 0.000 -2.77e+05 -2.32e+05 sqft_above 86.6902 2.269 38.211 0.000 82.243 91.137 condition 5.268e+04 2362.271 22.299 0.000 4.8e+04 5.73e+04 floors -2.753e+04 3705.453 -7.430 0.000 -3.48e+04 -2.03e+04 bedrooms -3.32e+04 2009.440 -16.520 0.000 -3.71e+04 -2.93e+04 view 8.806e+04 2067.874 42.584 0.000 8.4e+04 9.21e+04 grade 8.166e+04 2133.096 38.284 0.000 7.75e+04 8.58e+04 bathrooms 6688.8034 3271.002 2.045 0.041 277.397 1.31e+04 sqft_living 129.8780 2.236 58.090 0.000 125.496 134.260 sqft_basement 43.2078 2.817 15.340 0.000 37.687 48.729backward 알고리즘을 실행한 결과 총 12개의 변수가 선택되었습니다. R-squared의 값은 0.658입니다.
model=variable_selection(data,"price","stepwise") print(model.summary())OLS Regression Results ============================================================================== Dep. Variable: price R-squared: 0.596 Model: OLS Adj. R-squared: 0.596 Method: Least Squares F-statistic: 1.064e+04 Date: Thu, 25 Oct 2018 Prob (F-statistic): 0.00 Time: 22:27:47 Log-Likelihood: -2.9780e+05 No. Observations: 21613 AIC: 5.956e+05 Df Residuals: 21609 BIC: 5.956e+05 Df Model: 3 Covariance Type: nonrobust =============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------- Intercept -3.211e+07 5.48e+05 -58.634 0.000 -3.32e+07 -3.1e+07 sqft_living 192.6831 2.675 72.031 0.000 187.440 197.926 lat 6.644e+05 1.15e+04 57.556 0.000 6.42e+05 6.87e+05 grade 8.47e+04 2100.949 40.313 0.000 8.06e+04 8.88e+04stepwise 함수를 실행한 결과 총 3개의 독립변수가 선택되었습니다. R-squared의 값은 0.596입니다. stepwise 알고리즘의 경우 Empirical Study part에서 변수 제거율이 4가지 기법 중 가장 높았었는데 여기서도 역시 많은 변수를 제거한 것을 알 수 있었습니다.
model=GA(data,"price",10,30,2,100) print(model.summary())Dep. Variable: price R-squared: 0.652 Model: OLS Adj. R-squared: 0.652 Method: Least Squares F-statistic: 4501. Date: Thu, 25 Oct 2018 Prob (F-statistic): 0.00 Time: 22:32:41 Log-Likelihood: -2.9619e+05 No. Observations: 21613 AIC: 5.924e+05 Df Residuals: 21603 BIC: 5.925e+05 Df Model: 9 Covariance Type: nonrobust ================================================================================= coef std err t P>|t| [0.025 0.975] --------------------------------------------------------------------------------- Intercept -3.186e+07 5.17e+05 -61.680 0.000 -3.29e+07 -3.08e+07 lat 6.56e+05 1.09e+04 60.274 0.000 6.35e+05 6.77e+05 sqft_lot -0.0811 0.037 -2.217 0.027 -0.153 -0.009 condition 5.901e+04 2353.818 25.071 0.000 5.44e+04 6.36e+04 bedrooms -3.364e+04 2019.264 -16.658 0.000 -3.76e+04 -2.97e+04 grade 9.1e+04 2122.578 42.874 0.000 8.68e+04 9.52e+04 bathrooms -9077.1425 3061.573 -2.965 0.003 -1.51e+04 -3076.233 waterfront 8.072e+05 1.72e+04 46.911 0.000 7.73e+05 8.41e+05 sqft_living 202.9396 3.470 58.481 0.000 196.138 209.741 sqft_basement 20.1923 3.973 5.083 0.000 12.405 27.979GA 알고리즘을 수행한 결과 총 9개의 독립변수가 선택되었습니다. R-squared 값은 0.652입니다.
이렇게해서 4가지 기법을 모두 구현해보고 그 결과까지 확인하였습니다.
이 data의 경우에는 독립변수의 개수가 그리 많지 않았기 때문에 GA나 다른 기법간의 성능 차이가 그리 크지 않았고, 변수 소거율이 가장 높았던 stepwise 알고리즘이 성능은 R-squared 기준으로 가장 안좋았습니다.
오늘 post는 여기서 마치도록 하겠습니다. 읽어주셔서 감사합니다.